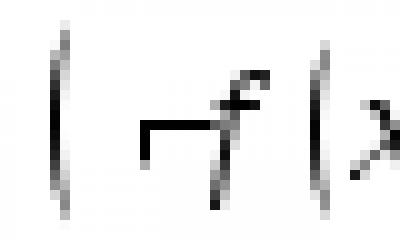Что касается функций (от лат. Functio - исполнение, осуществление) общения, то под ними понимают внешнее проявление свойств общения, те роли и задачи, которые оно выполняет в процессе жизнедеятельности индивида в социуме.
Известны различные подходы к классификации функций общения. Одни исследователи, рассматривая общение в контексте его органического единства с жизнью общества в целом и с непосредственными контактами людей и внутренней духовной жизнью человека.
Перечисленные функции, учитывая их интегральный характер, являются теми факторами, которые показывают существенно весомее роль общения для человека, чем просто передача информации. И знание этих интегральных функций, которые выполняет общение в процессе индивидуального развития человека, дает возможность выявить причины отклонений, нарушений процесса взаимодействия, неполноценной структуры и формы общения, в которые была вовлечен человек на протяжении всей жизни. Неадекватность форм общения человека в прошлом существенно влияет на его личностное развитие, определяет проблемы, которые встают перед ним сегодня.
Выделяют следующие функции:
общение является формой существования и проявления человеческой сущности, оно играет в коллективной деятельности людей коммуникативно-соединительную роль;
представляет собой важнейшую жизненную потребность человека, условие его благополучного существования, обладает психотерапевтическим, подтверждающим значением (подтверждение собственного «Я» другим лицом) в жизни индивида любого возраста.
Значительная часть исследователей выделяет функции общения, связанные с обменом информацией, взаимодействием и восприятием людьми друг друга.
Так, Б. Ломов выделяет в общении три функции: информационно-коммуникативную (заключается в любом обмене информацией), регуляционно-коммуникативную (регуляция поведения и регуляция совместной деятельности в процессе взаимодействия и аффективно-коммуникативную (регуляция эмоциональной сферы человека.
Информационно-коммуникативная функция охватывает процессы формирования, передачи и приема информации, ее реализация имеет несколько уровней: на первом осуществляется выравнивание различий в исходной информированности людей, которые вступают в психологический контакт; второй уровень предусматривает передачу информации и принятие решений (здесь общение реализует цели информирование, обучение и др.); третий уровень связан со стремлением человека понять других (общение, направленное на формирование оценок достигнутых результатов).
Вторая функция - регуляционно-коммуникативная - заключается в регуляции поведения. Благодаря общению человек осуществляет регуляцию не только собственного поведения, но и поведения других людей, и реагирует на их действия, то есть происходит процесс взаимного налаживания действий.
При таких условиях проявляются феномены, свойственные совместной деятельности, в частности, совместимость людей, их сработанность, осуществляется взаимная стимуляция и коррекция поведения. Эту функцию выполняют такие феномены, как имитация, внушение и др.
Третья функция - аффективно-коммуникативная - характеризует эмоциональную сферу человека, в которой выявляется отношение индивида к окружающей среде, в том числе и социальное.
Можно привести другую, немного подобную предыдущей, классификацию - четырех элементную модель (А. Реан), в которой общение образует: когнитивно-информационный (прием и передача информации), регулятивно-поведенческий (заостряет внимание на особенностях поведения субъектов, на взаимной регуляции их действий), аффективно-эмпатический (описывает общение как процесс обмена и регуляции на эмоциональном уровне) и социально-перцептивний компоненты (процесс взаимного восприятия, понимания и познания субъектов).
Ряд исследователей пытается расширить количество функций общения за счет их уточнения. В частности А. Брудный отличает инструментальную функцию, необходимую для обмена информацией в процессе управления и совместной работы; синдикативную которая находит свое отражение в сплочения малых и больших групп; трансляционную, необходимую для обучения, передачи знаний, способов деятельности, оценочных критериев; функцию самовыражения, сориентированную на поиск и достижение взаимного понимания.
Л. Карпенко по критерию «цель общения» выделяет еще восемь функций, которые реализуются в любом процессе взаимодействия и обеспечивают достижение в нем определенных целей:
контактную - установление контакта как состояния взаимной готовности к приему и передаче сообщения и поддержания связи во время взаимодействия в форме постоянной взаимо ориентированности;
информационную - обмен сообщениями (информацией, мнениями, решениями, замыслами, состояниями), т.е. прием - передача каких данных в ответ на полученный от партнера запрос;
побудительную - стимулирование активности партнера по общению, что направляет его на выполнение тех или иных действий;
координационную - взаимное ориентирование и согласование действий для организации совместной деятельности;
понимание - не только адекватное восприятие и понимание сущности сообщения, но и понимания партнерами друг друга;
амотивную - вызов у партнера по общению нужных эмоциональных переживаний и состояний, изменение с его помощью собственных переживаний и состояний;
установления отношений - осознание и фиксирование своего места в системе ролевых, статусных, деловых, межличностных и других связей, в которых предстоит действовать индивиду;
осуществления воздействия - изменение состояния, поведения, личностно-содержательных образований партнера (стремления, мнений, решений, действий, потребностей активности, норм и стандартов поведения и т.п.).
Среди функций общения ученые выделяют также социальные. Основная из них связана с управлением общественно-трудовыми процессами, другая - с установлением человеческих отношений.
В образовании сообщества заключается еще одна функция общения, которая направлена на поддержку социально-психологического единства в группах и связана с коммуникативной деятельностью (сущность деятельности в создании и поддержке конкретной взаимосвязи людей в группах) она допускает информационный обмен знаниями, отношениями и чувствами между людьми, т.е. имеет целью передачу-восприятие индивидом общественного опыта. Среди социальных функций общения важны функции подражания опыта и изменения личности (последняя осуществляется на основе механизмов восприятия, подражание, убеждение, заражение).
Изучение специфики общественно-политической деятельности позволяет выделить следующие основные функции общения в этой области знания (А. Деркач, Н. Кузьмина):
Социально-психологического отражения. Общение возникает как результат и как форма сознательного отражения партнерами особенностей протекания взаимодействия. Социально-психологический характер этого отражения проявляется в том, что прежде всего через языковую и другие формы сигнализации, элементы ситуации взаимодействия, восприняты и переработаны отдельным человеком, становятся реально действительными для его партнеров. Общение становится не столько обменом информацией, сколько процессом совместного взаимодействия и влияния. В зависимости от характера этого взаимовлияния происходит согласование, уточнение, взаимное дополнение содержательного и количественного аспектов «индивидуального» отображения с образованием групповой мысли, как формы коллективного мышления людей или, наоборот, столкновение мнений, их нейтрализация, сдерживание, как это бывает в межличностных конфликтах и неадекватных взаимовлияниях (прекращении общения);
Регулятивную. В процессе общения осуществляется непосредственное или косвенное влияние на члена группы с целью изменения или сохранения на том же уровне его поведения, действий, состояния, общей активности, особенностей восприятия, системы ценностей и отношений. Регулятивная функция позволяет организовать совместные действия, планировать и согласовывать, координировать и оптимизировать групповое взаимодействие членов коллектива. Регуляция поведения и деятельности является целью межличностной коммуникации как компонента предметной деятельности и конечным ее результатом. Именно осуществление этой важной функции общения позволяет оценить эффект общения, его производительность или непроизводительность;
Познавательную. Названая функция заключается в том, что в результате систематических контактов в ходе совместной деятельности члены группы овладевают различными знаниями о самих себе, своих друзьях, способах наиболее рационального решения поставленных перед ними задач. Овладение соответствующими умениями и навыками, возможна компенсация недостаточных знаний у отдельных членов группы и достижение ими необходимого взаимопонимания обеспечиваются именно познавательной функцией общения в сочетании с функцией социально-психологического отображения;
Экспрессивную. Различные формы вербального и невербального общения являются показателями эмоционального состояния и переживания члена группы часто вопреки логике и требованиям совместной деятельности. Это своеобразное проявление своего отношения к тому, что происходит через обращение к другому члену группы. Порой несовпадение в способах эмоционального регулирования может привести к отдалению партнеров, нарушению их межличностных отношений и даже к конфликтам;
Социального контроля. Способы решения задач, определенные формы поведения, эмоционального реагирования и отношений имеют нормативный характер, их регламентация посредством групповых и социальных норм обеспечивает необходимую целостность и организованность коллектива, согласованность совместных действий. Для поддержки согласованности и организованности групповой деятельности используются различные формы социального контроля. Межличностное общение в основном выступает в роли отрицательных (осуждение) или положительных (одобрение) санкций. Следует, однако, отметить, что не только одобрение или осуждение воспринимается участниками совместной деятельности в качестве наказания или поощрения. Нередко и отсутствие общения может восприниматься как та или иная санкция;
Социализации. Эта функция - одна из важнейших в работе субъектов деятельности. Приобщаясь к совместной деятельности и общения, члены группы осваивают коммуникативные умения и навыки, что позволяет им эффективно взаимодействовать с другими людьми. Хотя умение быстро оценить собеседника, ориентироваться в ситуации общения и взаимодействия, слушать и говорить играют важную роль в межличностной адаптации человека, еще большее значение имеют умение действовать в интересах группы, доброжелательное, заинтересованное и терпеливое отношение к другим членам группы.
Анализ особенностей общения в сфере деловых взаимоотношений также указывает на его многофункциональность (А. Панфилова, Е. Руденский):
инструментальная функция характеризует общение как социальный механизм управления, что дает возможность получить и передать информацию, необходимую для осуществления определенного действия, принятия решения и т.п.;
интегративной - используется как средство объединения деловых партнеров для совместного коммуникативного процесса;
функция самовыражения помогает самоутвердится, продемонстрировать личностный интеллект и психологический потенциал;
трансляционная - служит для передачи конкретных способов деятельности, оценок, мнений и др.;
функция социального контроля призвана регламентировать поведение, деятельность, а иногда (когда речь идет о коммерческой тайне) и языковые акции участников делового взаимодействия;
функция социализации способствует развитию навыков культуры делового общения; с помощью экспрессивной функции деловые партнеры пытаются выразить и понять эмоциональные переживания друг друга.
В. Панферов считает, что основные функции общения часто характеризуют, не прибегая к анализу функций человека как субъекта взаимодействия с другими людьми в совместной жизнедеятельности, что приводит к потере объективных основ их классификации. Анализируя классификацию функций общения, предложенную Б. Ломовым, исследователь ставит вопрос: «Исчерпывающими являются ряды функций по их количеству? Как много может быть таких рядов? О какой основной классификации может идти речь? Как разные основы связаны между собой?»
Пользуясь, случаем, напомним, что Б. Ломов выделил два ряда функций общения с различными основаниями. Первый из них включает три класса известных уже функций - информационно-коммуникативную, регуляционно-коммуникативную и аффективно-коммуникативную, а второй (по другой системе оснований) - охватывает организацию совместной деятельности, познания людьми друг друга, формирование и развитие межличностных отношений.
Отвечая на первый поставленный вопрос, В. Панферов среди основных функций общения выделяет шесть: коммуникативную, информационную, когнитивную (познавательная), эмотивную (ту, что вызывает душевные переживания), конативную (регуляцию, координацию взаимодействия), креативную (преобразовательная).
Все приведенные функции трансформируются в одну главную функцию общения - регуляторную, которая проявляется во взаимодействии индивида с другими людьми. И в этом смысле общение является механизмом соииально-психологической регуляции поведения людей в их совместной деятельности. Выделенные функции, по мнению исследователя, следует рассматривать как одно из оснований для классификации всех других функций человека как субъекта общения.
Общение всегда рассматривалось как полифункциональный процесс. Функции общения психологи определяют по разным критериям: эмоциональная, информационная, социализирующая, связующая, трансляционная, направленная на самопознание (А. В. Мудрик), установление общности, самоопределение (А. Б. Добрович), самовыражение (А. А. Брудный), сплочение и др. Чаще всего в психологии функции общения рассматривают в соответствии с моделью отношений "человек-деятельность-общество".
Можно выделить пять основных его функций: прагматическая, формирующая, подтверждающая, организация и поддержание межличностных отношений, внутриличностная (рис. 7).
В прагматической функции общение выступает как важнейшее условие объединения людей в процессе любой совместной деятельности. О том, какие разрушительные последствия для деятельности людей имеет невыполнение этого условия, повествуется в знаменитом библейском сюжете о строительстве Вавилонской башни.
Рис. 7.
Большая роль принадлежит формирующей функции общения. Общение ребенка и взрослого это не просто процесс передачи первому суммы умений, навыков и знаний, которые он механически усваивает, а сложный процесс взаимного влияния, обогащения и изменения. Жизненно необходимая роль общения ярко проявляется в следующем примере. В 30-х гг. XX в. в США был проведен эксперимент в двух клиниках, в которых дети лечились от серьезных, плохо излечимых заболеваний. Условия в обеих клиниках были одинаковые, но с некоторым различием: в одной больнице родственников к малышам не пускали, опасаясь инфекции, а в другой – в определенные часы родители могли пообщаться и поиграть с ребенком в специально отведенной комнате. Через несколько месяцев сравнили показатели эффективности лечения. В первом отделении коэффициент смертности приблизился к одной трети, несмотря на усилия врачей. Во втором отделении, где малышей лечили теми же средствами и методами, не умер ни один ребенок.
Функция подтверждения в процессе общения дает возможность познать, утвердить себя. Желая утвердиться в своем существовании и своей ценности, человек ищет точку опоры в другом человеке. Повседневный опыт человеческого общения изобилует процедурами, организованными по принципу подтверждения: ритуалы знакомства, приветствия, именования, оказание различных знаков внимания. Известный английский психиатр Р. Д. Лейнг видел в не подтверждении универсальный источник многих психических заболеваний, прежде всего – шизофрении.
Межличностная для любого человека связано с оцениванием людей и установлением определенных эмоциональных отношений – либо позитивных, либо негативных. Поэтому эмоциональное отношение к другому человеку может быть выражено в терминах "симпатии – антипатии", что накладывает свой отпечаток не только на личностное, но и на деловое общение.
Внутриличностная функция рассматривается как универсальный способ мышления человека. Л. С. Выготский отмечал в связи с этим, что "человек и наедине с самим собой сохраняет функцию общения".
Итак, ведущее значение общения в жизнедеятельности человека состоит в том, что оно является средством организации совместной деятельности людей и способом удовлетворения потребности человека в другом человеке, живом их контакте.
Общение как социально-психологический феномен – это контакт между людьми, который осуществляется посредством языка и речи, имеет разные формы проявления. Язык – система словесных знаков, средство, с помощью которого осуществляется общение между людьми. Использование языка с целью общения людей называют речью. В зависимости от особенностей общения выделяют различные его виды (рис. 8).
По контакту с собеседником общение может быть непосредственным и опосредованным.
Непосредственное общение (прямое) – это естественное общение, когда субъекты взаимодействия находятся рядом и общаются посредством речи, мимики и жестов.

Рис. 8.
Данный вид общения является наиболее полноценным, потому что индивиды в процессе его получают максимальную информацию друг о друге.
Опосредованное (косвенное) общение осуществляется в ситуациях, когда индивиды отдалены друг от друга временем или расстоянием. Например: разговор по телефону, переписка. Опосредованное общение это неполный психологический контакт, когда обратная связь затруднена.
Общение может быть межличностным или массовым. Массовое общение представляет собой множественные контакты незнакомых людей, а также коммуникацию, опосредованную различными видами массовой информации. Оно может быть прямым и опосредованным. Прямое массовое общение наблюдается на митингах, собраниях, демонстрациях, во всех больших социальных группах: толпе, публике, аудитории. Опосредованное массовое общение имеет односторонний характер и связано с массовой культурой и средствами массовой коммуникации.
По критерию равноправия партнеров в межличностном общении (рис. 9) выделяют два типа: диалогическое и монологическое.
Диалогическое общение – равноправное субъект-субъектное взаимодействие, имеющее целью взаимное познание, стремление к реализации целей каждого партнера.
Монологическое общение реализуется при неравноправных позициях партнеров и представляет собой субъект-объектные отношения. Оно может быть императивным и манипулятивным. Императивное общение – авторитарная, директивная форма взаимодействия с партнером с целью достижения контроля над его поведением, установками, мыслями и принуждения к определенным действиям или решениям. Причем цель эта не завуалирована. Манипулятивное общение – форма межличностного общения, при которой воздействие на партнера по общению осуществляется скрытно для достижения своих намерений.

Рис. 9.
Выделяют два типа коммуникаций – ролевую и личностную. В ролевом общении люди действуют, исходя из занимаемого статуса. Например, ролевым будет общение учителя с учениками, начальника цеха с рабочими и т.д. Ролевое общение регламентировано принятыми в обществе правилами и спецификой обращения. Личностное общение зависит от индивидуальных особенностей людей и взаимоотношений между ними.
Общение может быть кратковременным или длительным в зависимости от целей, содержания деятельности, индивидуальных особенностей собеседников, их симпатий, антипатий и т.д.
Обмен информацией может происходить посредством вербального и невербального взаимодействия. Вербальное общение происходит посредством речи, невербальное – с помощью паралингвистических средств передачи информации (громкость речи, тембр голоса, жесты, мимика, позы).
Общение осуществляется на разных уровнях. Уровни общения определяются общей культурой взаимодействующих объектов, их индивидуальными и личностными характеристиками, особенностями ситуации, социальным контролем, ценностными ориентациями общающихся, их отношением друг к другу (рис. 10).

Рис. 10.
Самый примитивный уровень общения – фатический (от лат. fatuus – глупый). Он предполагает простой обмен репликами для поддержания разговора, не имеет глубокого смысла. Такое общение необходимо в стандартизированных условиях либо определяется этикетными нормами.
Информационный уровень общения предполагает обмен интересной для собеседников новой информацией, являющейся источником эмоциональной, мыслительной, поведенческой активности человека.
Личностный уровень общения характеризует такое взаимодействие, при котором субъекты способны к глубокому самораскрытию и постижению сущности другого человека, самого себя и окружающего мира. Он построен на позитивном отношении к себе, другим людям и окружающему миру в целом. Это высший духовный уровень общения.
В данном подразделе мы вводим декартовы произведения, отношения, функции и графы. Изучаем свойства этих математических моделей и связи между ними.
Декартово произведение и перечисление его элементов
Декартовым произведением множеств A и B называется множество, состоящее из упорядоченных пар: A ´ B = {(a ,b ): (a Î A ) & (b Î B )}.
Для множеств A 1 , …, A n декартово произведение определяется по индукции:
В случае произвольного множества индексов I декартово произведение семейства множеств {A i } i Î I определяется как множество, состоящее из таких функций f: I ® A i , что для всех i Î I верно f(i) Î A i .
Теорема 1
Пусть A и B – конечные множества. Тогда | A ´B| = | A| ×| B|.
Доказательство
Пусть A = { a 1 , …, a m } , B = { b 1 , …, b n } . Элементы декартового произведения можно расположить с помощью таблицы
(a 1 ,b 1), (a 1 ,b 2), …, (a 1 ,b n) ;
(a 2 ,b 1), (a 2 ,b 2), …, (a 2 ,b n) ;
(a m ,b 1), (a m ,b 2),…, (a m ,b n) ,
состоящей из n столбцов, каждый из которых состоит из m элементов. Отсюда | A ´B|= mn .
Следствие 1
Доказательство
C помощью индукции по n . Пусть формула верна для n . Тогда
Отношения
Пусть n ³1 – положительное целое число и A 1 , …, A n – произвольные множества. Отношением между элементами множеств A 1 , …, A n или n-арным отношением называется произвольное подмножество .
Бинарные отношения и функции
Бинарным отношением между элементами множеств A и B (или, коротко, между A и B ) называется подмножество R Í A ´B .
Определение 1
Функцией или отображением называется тройка, состоящая из множеств A и B и подмножества f Í A ´ B (графика функции ), удовлетворяющего следующим двум условиям;
1) для любого x Î A существует такой y Î f , что (x, y) Î f ;
2) если (x, y) Î f и (x, z) Î f , то y = z.
Легко видеть, что f Í A ´ B будет тогда и только определять функцию, когда для любого x Î A существует единственный y Î f , что (x ,y ) Î f . Этот y обозначим через f (x ).
Функция называется инъекцией , если для любых x, x’ Î A , таких что x ¹ x’ , имеет место f(x) ¹ f(x’) . Функция называется сюръекцией , если для каждого y Î B существует такой x Î A , что f (x ) = y . Если функция является инъекцией и сюръекцией, то она называется биекцией .
Теорема 2
Для того чтобы функция была биекцией, необходимо и достаточно существования такой функции , что fg = Id B и gf = Id A .
Доказательство
Пусть f – биекция. В силу сюръективности f для каждого y Î B можно выбрать элемент x Î A , для которого f (x ) = y . В силу инъективности f , этот элемент будет единственным, и мы обозначим его через g (y ) = x . Получим функцию .
По построению функции g
, имеют место равенства f
(g
(y
)) = y
и g
(f
(x
)) = x
. Значит, верно fg =
Id B
и gf =
Id A
. Обратное очевидно: если fg =
Id B
и gf =
Id A ,
то f
– сюръекция в силу f
(g
(y
)) = y
, для каждого y
Î B
. В этом случае из будет следовать ![]() , и значит . Следовательно, f
– инъекция. Отсюда вытекает, что f
– биекция.
, и значит . Следовательно, f
– инъекция. Отсюда вытекает, что f
– биекция.
Образ и прообраз
Пусть – функция. Образом подмножества X Í A называется подмножество f(X) = { f(x): x Î X} Í B. Для Y Í B подмножество f - -1 (Y) ={ x Î A: f(x) Î Y} называется прообразом подмножества Y .
Отношения и графы
Бинарные отношения можно наглядно показать с помощью ориентированных графов .
Определение 2
Ориентированным графом называется пара множеств (E, V) вместе с парой отображений s, t: E ® V . Элементы множества V изображаются точками на плоскости и называются вершинами . Элементы из E называются направленными ребрами или стрелками . Каждый элемент e Î E изображается в виде стрелки (возможно, криволинейной), соединяющей вершину s(e) с вершиной t(e) .
Произвольному бинарному отношению R Í V ´ V соответствует ориентированный граф с вершинами v Î V , стрелками которого являются упорядоченные пары (u, v) Î R . Отображения s, t: R ® V определяются по формулам:
s(u, v) = u и t(u, v) = v .
Пример 1
Пусть V = {1,2,3,4}
.
Рассмотрим отношение
R = {(1,1), (1,3), (1.4), (2,2), (2,3), (2,4), (3,3), (4,4)} .
Ему будет соответствовать ориентированный граф (рис. 1.2). Стрелками этого граф будут пары (i, j) Î R .

Рис. 1.2. Ориентированный граф бинарного отношения
В полученном ориентированном графе любая пара вершин соединяется не более чем одной стрелкой. Такие ориентированные графы называются простыми . Если не рассматривать направление стрелок, то мы приходим к следующему определению:
Определение 3
Простым (неориентированным) графом G = (V, E) называется пара, состоящая из множества V и множества E , состоящего из некоторых неупорядоченных пар {v 1 , v 2 } элементов v 1 , v 2 Î V таких, что v 1 ¹ v 2 . Эти пары называются ребрами , а элементы из V – вершинами .

Рис. 1.3. Простой неориентированный граф K 4
Множество E определяет бинарное симметричное антирефлексивное отношение, состоящее из пар (v 1 , v 2 ), для которых {v 1 , v 2 } Î E . Вершины простого графа изображаются как точки, а ребра – как отрезки. На рис. 1.3 изображен простой граф с множеством вершин
V = {1, 2, 3, 4}
и множеством ребер
E = {{1,2}, {1,3},{1,4}, {2,3}, {2,4}, {3, 4}}.
Операции над бинарными отношениями
Бинарным отношением между элементами множеств A и B называется произвольное подмножество R Í A ´ B . Запись aRb (при a Î A , b Î B ) означает, что (a, b) Î R .
Определены следующие операции над отношениями R Í A ´ A :
· R -1 = {(a,b): (b,a) Î R} ;
· R ° S = {(a,b): ($ x Î A)(a,x) Î R & (x,b) Î R} ;
· R n = R °(R n -1) ;
Пусть Id A = {(a, a): a Î A} – тождественное отношение. Отношение R Í X ´ X называется:
1) рефлексивным , если (a, a) Î R для всех a Î X ;
2) антирефлексивным , если (a, a) Ï R для всех a Î X ;
3) симметричным , если для всех a, b Î X верна импликация aRb Þ bRa ;
4) антисимметричным , если aRb & bRa Þ a= b ;
5) транзитивным , если для всех a, b, c Î X верна импликация aRb & bRc Þ aRc ;
6) линейным , для всех a, b Î X верна импликация a ¹ b Þ aRb Ú bRa .
Обозначим Id A через Id . Легко видеть, что имеет место следующее.
Предложение 1
Отношение R Í X ´ X :
1) рефлексивно Û Id Í R ;
2) антирефлексивно Û R Ç Id= Æ ;
3) симметрично Û R = R -1 ;
4) антисимметрично Û R Ç R -1 Í Id ;
5) транзитивно Û R ° R Í R ;
6) линейно Û R È Id È R -1 = X ´ X .
Матрица бинарного отношения
Пусть A = {a 1 , a 2 , …, a m } и B = {b 1 , b 2 , …, b n } – конечные множества. Матрицей бинарного отношения R Í A ´ B называется матрица с коэффициентами:
![]()
Пусть A – конечное множество, |A | = n и B = A . Рассмотрим алгоритм вычисления матрицы композиции T = R ° S отношений R , S Í A ´ A . Обозначим коэффициенты матриц отношений R , S и T соответственно через r ij , s ij и t ij .
Поскольку свойство (a i ,a k )ÎT равносильно существованию такого a j Î A , что (a i ,a j )ÎR и (a j ,a k ) Î S , то коэффициент t ik будет равен 1, если и только если существует такой индекс j , что r ij = 1 и s jk = 1. В остальных случаях t ik равен 0. Следовательно, t ik = 1 тогда и только тогда, когда .
Отсюда вытекает, что для нахождения матрицы композиции отношений нужно перемножить эти матрицы и в полученном произведении матриц ненулевые коэффициенты заменить на единицы. Следующий пример показывает, как этим способом вычисляется матрица композиции.
Пример 2
Рассмотрим бинарное отношение на A = {1,2,3} , равное R = {(1,2),(2,3)} . Запишем матрицу отношения R . Согласно определению, она состоит из коэффициентов r 12 = 1, r 23 = 1 и остальных r ij = 0. Отсюда матрица отношения R равна:
Найдем отношение R ° R . С этой целью умножим матрицу отношения R на себя:
 .
.
Получаем матрицу отношения:
Следовательно, R ° R = {(1,2),(1,3),(2,3)}.
Из предложения 1 вытекает следующее следствие.
Следствие 2
Если A = B , то отношение R на A :
1) рефлексивно, если и только если все элементы главной диагонали матрицы отношения R равны 1;
2) антирефлексивно, если и только если все элементы главной диагонали матрицы отношения R равны 0;
3) симметрично, если и только если матрица отношения R симметрична;
4) транзитивно, если и только если каждый коэффициент матрицы отношения R ° R не больше соответствующего коэффициента матрицы отношения R.
Упражнения.
1) С помощью формулы бинома Ньютона при a = 1, b = i вычислить +++…, +++…, +++…, +++…
2) С помощью формулы Муавра вычислить устно sin 4j и cos 5j .
Лекция 3.
- СООТВЕТСТВИЯ. ФУНКЦИИ. ОТНОШЕНИЯ. ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ
Определение. Будем говорить, что на множестве Х задано бинарное отношение R , если " x, y Î X мы можем определить (по какому-нибудь правилу) находятся эти элементы в отношении R или нет.
Определим понятие отношения более строго.
Введем понятие декартова (прямого) произведение A´B произвольных множеств A и B.
По определению A´B = { (a, b), a Î A , bÎ B}. Аналогично определяется декартово произведение 3-х, 4-х и произвольного числа множеств. По определению A´A´ …´A = A n .
Определения .
1. Соответствием S из множества A в множество B называется подмножество S Í A´B. Тот факт, что элементы aÎ A, bÎ B находятся в соответствии S, мы будем записывать в виде (a, b) Î S или в виде aSb.
2. Естественным образом для соответствий S 1 и S 2 определяются S 1 ∩S 2 и S 1 U S 2 – как пересечение и объединение подмножеств. Как и для любых подмножеств определяется понятие включения соответствий S 1 Í S 2 . Так S 1 Í S 2 Û
из a S 1 b Þ a S 2 b.
3. Для соответствий S 1 Í A´B и S 2 Í B´C определим композицию соответствий S 1 *S 2 Í A´С. Будем считать, что для элементов aÎ A, сÎ С по определению a S 1 *S 2 с Û $ bÎ B такой, что a S 1 b и b S 2 с.
4. Для соответствия S Í A´B определим соответствие
S -1 Í B´A так: по определению bS -1 a Û a S b.
5. Пусть по определению соответствие D A Í A´A,
D A ={(a,a), aÎ A}.
6. Соответствие F из множества A в множество B называется функцией, определенной на A, со значениями в B (или отображением из A в B ), если " aÎ A $! bÎ B такой, что aFb. В этом случае будем писать также aF = b или, более привычно, Fa = b. В этом определении функция отождествляется со своим графиком. В наших обозначениях aF 1 *F 2 с можно записать в виде с = (aF 1)F 2 . Композиция F 2 F 1 функций означает по определению, что (F 2 F 1)(a)= F 2 (F 1 (a)). Таким образом, F 2 F 1 = F 1 *F 2 .
7. Для отображения F из A в B образом подмножества A 1 Í A
называется подмножество F(A 1)= {F(a)| aÎ A 1 } Í B, а прообразом подмножества B 1 Í B называется подмножество
F -1 (B 1)= { aÎ A | F(a) Î B 1 } Í A .
8. Отображение F из A в B называется инъекцией , если из
a 1 ¹ a 2 Þ Fa 1 ¹ Fa 2 .
9. Отображение F из A в B называется сюръекцией , если
" bÎ B $ aÎ A такой, что Fa = b.
10. Отображение F из A в B называется биекцией или взаимнооднозначным отображением , если F – инъекция и сюръекция одновременно.
11. Биекция конечного (а иногда и бесконечного) множества называется подстановкой .
12. Бинарным отношением на множестве Х называется подмножество R Í X´X. Тот факт, что элементы x, y Î X находятся в отношении R, мы будем записывать в виде (x, y) Î R или в виде xRy.
Отношения. Основные понятия и определения
Определение 2.1. Упорядоченной парой <x , y > называется совокупность двух элементов x и y , расположенных в определенном порядке.
Две упорядоченные пары <x , y > и <u , v> равны межу собой тогда и только тогда, когда x = u и y = v.
Пример 2.1 .
<a , b >, <1, 2>, <x , 4> – упорядоченные пары.
Аналогично можно рассматривать тройки, четверки, n -ки элементов <x 1 , x 2 , … x n >.
Определение 2.2. Прямым (или декартовым )произведением двух множеств A и B называется множество упорядоченных пар, таких, что первый элемент каждой пары принадлежит множеству A , а второй – множеству B :
A ´ B = {<a , b >, ç a Î А и b Ï В }.
В общем случае прямым произведением n множеств А 1 , А 2 ,… А n называется множество А 1 ´ А 2 ´ …´ А n , состоящее из упорядоченных наборов элементов <a 1 , a 2 , …, a n > длины n , таких, что i- ый a i принадлежит множеству А i , a i Î А i .
Пример 2.2 .
Пусть А = {1, 2}, В = {2, 3}.
Тогда A ´ B = {<1, 2>, <1, 3>,<2, 2>,<2, 3>}.
Пример 2.3 .
Пусть А = {x ç0 £ x £ 1} и B = {y ç2 £ y £ 3}
Тогда A ´ B = {< x , y >, ç0 £ x £ 1и2 £ y £ 3}.
Таким образом, множество A ´ B состоит из точек, лежащих внутри и на границе прямоугольника, образованного прямыми x = 0 (ось ординат), x = 1, y = 2и y = 3.
Французский математик и философ Декарт впервые предложил координатное представление точек плоскости. Это исторически первый пример прямого произведения.
Определение 2.3. Бинарным (или двуместным )отношением r называется множество упорядоченных пар.
Если пара <x , y > принадлежит r , то это записывается следующим образом: <x , y > Î r или, что то же самое, xr y .
Пример2.4 .
r = {<1, 1>, <1, 2>, <2, 3>}
Аналогично можно определить n -местное отношение как множество упорядоченных n -ок.
Так как бинарное отношение – множество, то способы задания бинарного отношения такие же, как и способы задания множества (см. разд. 1.1). Бинарное отношение может быть задано перечислением упорядоченных пар или указанием общего свойства упорядоченных пар.
Пример 2.5 .
1. r = {<1, 2>, <2, 1>, <2, 3>} – отношение задано перечислением упорядоченных пар;
2. r = {<x , y > çx + y = 7, x , y – действительные числа} – отношение задано указанием свойства x + y = 7.
Кроме того, бинарное отношение может быть задано матрицей бинарного отношения . Пусть А = {a 1 , a 2 , …, a n } – конечное множество. Матрица бинарного отношения C есть квадратная матрица порядка n , элементы которой c ij определяются следующим образом:
Пример 2.6 .
А = {1, 2, 3, 4}. Зададим бинарное отношение r тремя перечисленными способами.
1. r = {<1, 2>, <1, 3>, <1, 4>, <2, 3>, <2, 4>, <3, 4>} – отношение задано перечислением всех упорядоченных пар.
2. r = {< a i , a j > ça i < a j ; a i , a j Î А } – отношение задано указанием свойства "меньше" на множестве А .
3. – отношение задано матрицей бинарного отношения C .
Пример 2.7 .
Рассмотрим некоторые бинарные отношения.
1. Отношения на множестве натуральных чисел.
а) отношение £ выполняется для пар <1, 2>, <5, 5>, но не выполняется для пары <4, 3>;
б) отношение "иметь общий делитель, отличный от единицы" выполняется для пар <3, 6>, <7, 42>, <21, 15>, но не выполняется для пары <3, 28>.
2. Отношения на множестве точек действительной плоскости.
а) отношение "находиться на одинаковом расстоянии от точки (0, 0)" выполняется для точек (3, 4) и (–2, Ö21), но не выполняется для точек (1, 2) и (5, 3);
б) отношение "быть симметричным относительно оси OY " выполняется для всех точек (x , y ) и (–x , –y ).
3. Отношения на множестве людей.
а) отношение "жить в одном городе";
б) отношение "учиться в одной группе";
в) отношение "быть старше".
Определение 2.4. Областью определения бинарного отношения r называется множество D r = {x çсуществует y, что xr y}.
Определение 2.5. Областью значений бинарного отношения r называется множество R r = {y çсуществует x, что xr y}.
Определение 2.6. Областью задания бинарного отношения r называется множество M r = D r ÈR r .
Используя понятие прямого произведения, можно записать:
r Î D r ´ R r
Если D r = R r = A , то говорят, что бинарное отношение r задано на множестве A .
Пример 2.8 .
Пусть r = {<1, 3>, <3, 3>, <4, 2>}.
Тогда D r = {1, 3, 4}, R r = {3, 2}, M r = {1, 2, 3, 4}.
Операции над отношениями
Так как отношения являются множествами, то все операции над множествами справедливы для отношений.
Пример 2.9 .
r 1 = {<1, 2>, <2, 3>, <3, 4>}.
r 2 = {<1, 2>, <1, 3>, <2, 4>}.
r 1 È r 2 = {<1, 2>, <1, 3>, <2, 3>, <2, 4>, <3, 4>}.
r 1 Ç r 2 = {<1, 2>}.
r 1 \ r 2 = {<2, 3>, <3, 4>}.
Пример 2.10 .
Пусть R – множество действительных чисел. Рассмотрим на этом множестве следующие отношения:
r 1 – " £ "; r 2 – " = "; r 3 – " < "; r 4 – " ³ "; r 5 – " > ".
r 1 = r 2 È r 3 ;
r 2 = r 1 Ç r 4 ;
r 3 = r 1 \ r 2 ;
r 1 = ;
Определим еще две операции над отношениями.
Определение 2.7. Отношение называется обратным к отношению r (обозначается r – 1), если
r – 1 = {<x , y > ç< y, x > Î r }.
Пример 2.11 .
r = {<1, 2>, <2, 3>, <3, 4>}.
r – 1 = {<2, 1>, <3, 2>, <4, 3>}.
Пример 2.12 .
r = {<x , y > ç x – y = 2, x , y Î R }.
r – 1 = {<x , y > ç< y, x > Î r } = r – 1 = {<x , y > çy – x = 2, x , y Î R } = {<x , y > ç– x + y = 2, x , y Î R }.
Определение 2.8. Композицией двух отношений r и s называется отношение
s r = {<x , z > çсуществует такое y , что <x , y > Î r и < y, z > Îs }.
Пример 2.13 .
r = {<x , y > çy = sinx }.
s = {<x , y > çy = Öx }.
s r = {<x , z > çсуществует такое y , что <x , y > Î r и < y, z > Îs } = {<x , z > çсуществует такое y , что y = sinx и z = Öy } = {<x , z > ç z = Ösinx }.
Определение композиции двух отношенийсоответствует определению сложной функции:
y = f (x ), z = g (y ) Þ z = g (f (x )).
Пример 2.14 .
r = {<1, 1>, <1, 2>, <1, 3>, <3, 1>}.
s = {<1, 2>, <1, 3>, <2, 2>, <3, 2>, <3, 3>}.
Процесс нахождения s r в соответствии с определением композиции удобно изобразить таблицей, в которой реализуется перебор всех возможных значений x , y , z . для каждой пары <x , y > Î r нужно рассмотреть все возможные пары < y, z > Îs (табл. 2.1).
Таблица 2.1
| <x , y > Î r | < y, z > Îs | <x , z > Îs r |
| <1, 1> <1, 1> <1, 2> <1, 3> <1, 3> <3, 1> <3, 1> | <1, 2> <1, 3> <2, 2> <3, 2> <3, 3> <1, 2> <1, 3> | <1, 2> <1, 3> <1, 2> <1, 2> <1, 3> <3, 2> <3, 3> |
Заметим, что первая, третья и четвертая, а также вторая и пятая строки последнего столбца таблицы содержат одинаковые пары. Поэтому получим:
s r = {<1, 2>, <1, 3>, <3, 2>, <3, 3>}.
Свойства отношений
Определение 2.9. Отношение r называется рефлексивным на множестве X , если для любого x Î X выполняется xr x .
Из определения следует, что всякий элемент < x , x > Î r .
Пример 2.15 .
а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <2, 2>, <3, 1>, <3, 3>}. Отношение r рефлексивно. Если X – конечное множество, то главная диагональ матрицы рефлексивного отношения содержит только единицы. Для нашего примера
б) Пусть X r отношение равенства. Это отношение рефлексивно, т.к. каждое число равно самому себе.
в) Пусть X – множество людей и r отношение "жить в одном городе". Это отношение рефлексивно, т.к. каждый живет в одном городе сам с собой.
Определение 2.10. Отношение r называется симметричным на множестве X , если для любых x , y Î X из xry следует yr x .
Очевидно, что r симметрично тогда и только тогда, когда r = r – 1 .
Пример 2.16 .
а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 1>, <3, 1>, <3, 3>}. Отношение r симметрично. Если X – конечное множество, то матрица симметричного отношения симметрична относительно главной диагонали. Для нашего примера
б) Пусть X – множество действительных чисел и r отношение равенства. Это отношение симметрично, т.к. если x равно y , то и y равно x .
в) Пусть X – множество студентов и r отношение "учиться в одной группе". Это отношение симметрично, т.к. если x учится в одной группе с y , то и y учится в одной группе с x .
Определение 2.11. Отношение r называется транзитивным на множестве X , если для любых x , y , z Î X из xry и yr z следует xr z .
Одновременное выполнение условий xry , yr z , xr z означает, что пара <x , z > принадлежит композиции r r . Поэтому для транзитивности r необходимо и достаточно, чтобы множество r r являлось подмножеством r , т. е. r r Í r .
Пример 2.17 .
а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <2, 3>, <1, 3>}. Отношение r транзитивно, т. к. наряду с парами <x , y >и <y , z >имеется пара<x , z >. Например, наряду с парами <1, 2>, и <2, 3> имеется пара <1, 3>.
б) Пусть X – множество действительных чисел и r отношение £ (меньше или равно). Это отношение транзитивно, т.к. если x £ y и y £ z , то x £ z .
в) Пусть X – множество людей и r отношение "быть старше". Это отношение транзитивно, т.к. если x старше y и y старше z , то x старше z .
Определение 2.12. Отношение r называется отношением эквивалентности на множестве X , если оно рефлексивно, симметрично и транзитивно на множестве X .
Пример 2.18 .
а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <2, 2>, <3, 3>}. Отношение r является отношением эквивалентности.
б) Пусть X – множество действительных чисел и r отношение равенства. Это отношение эквивалентности.
в) Пусть X – множество студентов и r отношение "учиться в одной группе". Это отношение эквивалентности.
Пусть r X .
Определение 2.13. Пусть r – отношение эквивалентности на множестве X и x Î X . Классом эквивалентности , порожденным элементом x , называется подмножество множества X , состоящее из тех элементов y Î X , для которых xry . Класс эквивалентности, порожденный элементом x , обозначается через [x ].
Таким образом, [x ] = {y Î X | xry }.
Классы эквивалентности образуют разбиение множества X , т. е. систему непустых попарно непересекающихся его подмножеств, объединение которых совпадает со всем множеством X .
Пример 2.19 .
а) Отношение равенства на множестве целых чисел порождает следующие классы эквивалентности: для любого элемента x из этого множества [x ] = {x }, т.е. каждый класс эквивалентности состоит из одного элемента.
б) Класс эквивалентности, порожденный парой <x , y > определяется соотношением:
[<x , y >] = .
Каждый класс эквивалентности, порожденный парой <x , y >, определяет одно рациональное число.
в) Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы.
Определение 2.14. Отношение r называется антисимметричным на множестве X , если для любых x , y Î X из xry и yr x следует x = y .
Из определения антисимметричности следует, что всякий раз, когда пара <x , y > принадлежит одновременно r и r – 1 , должно выполняться равенство x = y . Другими словами, r Ç r – 1 состоит только из пар вида < x , x >.
Пример 2.20 .
а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 2>, <2, 3>, <3, 3>}. Отношение r антисимметрично.
Отношение s = {<1, 1>, <1, 2>, <1, 3>, <2, 1>, <2, 3>, <3, 3>} неантисимметрично. Например, <1, 2> Îs, и <2, 1> Îs , но 1 ¹2.
б) Пусть X – множество действительных чисел и r отношение £ (меньше или равно). Это отношение антисимметрично, т.к. если x £ y , и y £ x , то x = y .
Определение 2.15. Отношение r называется отношением частичного порядка (или просто частичным порядком) на множестве X , если оно рефлексивно, антисимметрично и транзитивно на множестве X . Множество X в этом случае называют частично упорядоченным и указанное отношение часто обозначают символом £, если это не приводит к недоразумениям.
Отношение, обратное отношению частичного порядка будет, очевидно, отношением частичного порядка.
Пример 2.21 .
а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 2>, <2, 3>, <3, 3>}. Отношение r
б) Отношение А Í В на множестве подмножеств некоторого множества U есть отношение частичного порядка.
в) Отношение делимости на множестве натуральных чиселесть отношение частичного порядка.
Функции. Основные понятия и определения
В математическом анализе принято следующее определение функции.
Переменная y называется функцией от переменной x , если по некоторому правилу или закону каждому значению x соответствует одно определенное значение y = f (x ). Область изменения переменной x называется областью определения функции, а область изменения переменной y – областью значений функции. Если одному значению x соответствует несколько (и даже бесконечно много значений y ), то функция называется многозначной. Впрочем, в курсе анализа функций действительных переменных избегают многозначных функций и рассматривают однозначные функции.
Рассмотрим другое определение функции с точки зрения отношений.
Определение 2.16. Функцией называется любое бинарное отношение, которое не содержит двух пар с равными первыми компонентами и различными вторыми.
Такое свойство отношения называется однозначностью или функциональностью .
Пример 2.22 .
а) {<1, 2>, <3, 4>, <4, 4>, <5, 6>} – функция.
б) {<x , y >: x , y Î R , y = x 2 } – функция.
в) {<1, 2>, <1, 4>, <4, 4>, <5, 6>} – отношение, но не функция.
Определение 2.17. Если f – функция, то D f – область определения , а R f – область значений функции f .
Пример 2.23 .
Для примера 2.22 а) D f – {1, 3, 4, 5}; R f – {2, 4, 6}.
Для примера 2.22 б) D f = R f = (–¥, ¥).
Каждому элементу x D f функция ставит в соответствие единственный элемент y R f . Это обозначается хорошо известной записью y = f (x ). Элемент x называется аргументом функции или прообразом элемента y при функции f , а элемент y значением функции f на x или образом элемента x при f .
Итак, из всех отношений функции выделяются тем, что каждый элемент из области определения имеет единственный образ.
Определение 2.18. Если D f = X и R f = Y , то говорят, что функция f определена на X и принимает свои значения на Y , а f называют отображением множества X на Y (X ® Y ).
Определение 2.19. Функции f и g равны, если их область определения – одно и то же множество D , и для любого x Î D справедливо равенство f (x ) = g (x ).
Это определение не противоречит определению равенства функций как равенства множеств (ведь мы определили функцию как отношение, т. е. множество): множества f и g равны, тогда и только тогда, когда они состоят из одних и тех же элементов.
Определение 2.20. Функция (отображение) f называется сюръективной или просто сюръекцией , если ля любого элемента y Y существует элемент x Î X , такой, что y = f (x ).
Таким образом, каждая функция f является сюръективным отображением (сюръекцией) D f ® R f .
Если f – сюръекция, а X и Y – конечные множества, то ³ .
Определение 2.21. Функция (отображение) f называется инъективной или просто инъекцией или взаимно однозначной , если из f (a ) = f (b ) следует a = b .
Определение 2.22. Функция (отображение) f называется биективной или просто биекцией , если она одновременно инъективна и сюръективна.
Если f – биекция, а X и Y – конечные множества, то = .
Определение 2.23. Если область значений функции D f состоит из одного элемента, то f называется функцией-константой .
Пример 2.24 .
а) f (x ) = x 2 есть отображение множества действительных чисел на множество неотрицательных действительных чисел. Т.к. f (–a ) = f (a ), и a ¹ –a , то эта функция не является инъекцией.
б) Для каждого x R = (– , ) функция f (x ) = 5 – функция-константа. Она отображает множество R на множество {5}. Эта функция сюръективна, но не инъективна.
в) f (x ) = 2x + 1 является инъекцией и биекцией, т.к. из 2x 1 +1 = 2x 2 +1 следует x 1 = x 2 .
Определение 2.24. Функция, реализующая отображение X 1 ´ X 2 ´...´ X n ®Y называется n-местной функцией.
Пример 2.25 .
а) Сложение, вычитание, умножение и деление являются двуместными функциями на множестве R действительных чисел, т. е. функциями типа R 2 ® R .
б) f (x , y ) = – двуместная функция, реализующая отображение R ´ (R \ )® R . Эта функция не является инъекцией, т.к. f (1, 2) = f (2, 4).
в) Таблица выигрышей лотереи задает двуместную функцию, устанавливающую соответствие между парами из N 2 (N – множество натуральных чисел) и множеством выигрышей.
Поскольку функции являются бинарными отношениями, то можно находить обратные функции и применять операцию композиции. Композиция любых двух функций есть функция, но не для каждой функции f отношение f –1 является функцией.
Пример 2.26 .
а) f = {<1, 2>, <2, 3>, <3, 4>, <4, 2>} – функция.
Отношение f –1 = {<2, 1>, <3, 2>, <4, 3>, <2, 4>} не является функцией.
б) g = {<1, a >, <2, b >, <3, c >, <4, D >} – функция.
g -1 = {<a , 1>, <b , 2>, <c , 3>, <D , 4>} тоже функция.
в) Найдем композицию функций f из примера а) и g -1 из примера б). Имеем g -1f = {<a , 2>, <b , 3>, <c , 4>, <d , 2>}.
fg -1 = Æ.
Заметим, что (g -1f )(a ) = f (g -1 (a )) = f (1) = 2; (g -1f )(c ) = f (g -1 (c )) = f (3) = 4.
Элементарной функцией в математическом анализе называется всякая функция f , являющаяся композицией конечного числа арифметических функций, а также следующих функций:
1) Дробно-рациональные функции, т.е. функции вида
a 0 + a 1 x + ... + a n x n
b 0 + b 1 x + ... + b m x m .
2) Степенная функция f (x ) = x m , где m – любое постоянное действительное число.
3) Показательная функция f (x ) = e x .
4) логарифмическая функция f (x ) = log a x , a >0, a 1.
5) Тригонометрические функции sin, cos, tg, ctg, sec, csc .
6) Гиперболические функции sh, ch, th, cth .
7) Обратные тригонометрические функции arcsin , arccos и т.д.
Например, функция log 2 (x 3 +sincos 3x ) является элементарной, т.к. она есть композиция функций cosx , sinx , x 3 , x 1 + x 2 , logx , x 2 .
Выражение, описывающее композицию функций, называется формулой.
Для многоместной функции справедлив следующий важный результат, полученный А. Н. Колмогоровым и В. И. Арнольдом в 1957 г. и являющийся решением 13-ой проблемы Гильберта:
Теорема. Всякая непрерывная функция n переменных представима в виде композиции непрерывных функций двух переменных.
Способы задания функций
1. Наиболее простой способ задания функций – это таблицы (табл. 2.2):
Таблица 2.2
Однако, таким образом могут быть заданы функции, определенные на конечных множествах.
Если функция, определенная на бесконечном множестве (отрезке, интервале), задана в конечном числе точек, например, в виде тригонометрических таблиц, таблиц специальных функций и т.п., то для вычисления значений функций в промежуточных точках пользуются правилами интерполяции.
2. Функция может быть задана в виде формулы, описывающей функцию как композицию других функций. Формула задает последовательность вычисления функции.
Пример 2.28 .
f (x ) = sin (x + Öx ) является композицией следующих функций:
g (y ) = Öy ; h (u, v) = u + v; w (z ) = sinz.
3. Функция может быть задана в виде рекурсивной процедуры. Рекурсивная процедура задает функцию, определенную на множестве натуральных чисел, т. е. f (n ), n = 1, 2,... следующим образом: а) задается значение f (1) (или f (0)); б) значение f (n + 1) определяется через композицию f (n ) и других известных функций. Простейшим примером рекурсивной процедуры является вычисление n !: а) 0! = 1; б) (n + 1)! = n !(n + 1). Многие процедуры численных методов являются рекурсивными процедурами.
4. Возможны способы задания функции, не содержащие способа вычисления функции, а только описывающие ее. Например:
f M (x ) =
Функция f M (x ) – характеристическая функция множества M .
Итак, по смыслу нашего определения, задать функцию f – значит задать отображение X ® Y , т.е. определить множество X ´Y , поэтому вопрос сводится к заданию некоторого множества. Однако можно определить понятие функции, не используя языка теории множеств, а именно: функция считается заданной, если задана вычислительная процедура, которая по заданному значению аргумента находит соответствующее значение функции. Функция, определенная таким образом, называется вычислимой.
Пример 2.29 .
Процедура определения чисел Фибоначчи , задается соотношением
F n = F n- 1 + F n- 2 (n ³ 2) (2.1)
с начальными значениями F 0 = 1, F 1 = 1.
Формула (2.1) вместе с начальными значениями определяет следующий ряд чисел Фибоначчи:
| n | 0 1 2 3 4 5 6 7 8 9 10 11 … |
| F n | 1 1 2 3 5 8 13 21 34 55 89 144 … |
Вычислительная процедура определения значения функции по заданному значению аргумента есть не что иное, как алгоритм .
Контрольные вопросы к теме 2
1. Укажите способы задания бинарного отношения.
2. Главная диагональ матрицы какого отношения содержит только единицы?
3. Для какого отношения r всегда выполняется условие r = r – 1 ?
4. Для какого отношения r всегда выполняется условие r r Í r .
5. Ввести отношения эквивалентности и частичного порядка на множестве всех прямых на плоскости.
6. Укажите способы задания функций.
7. Какое из следующих утверждений справедливо?
а) Всякое бинарное отношение есть функция.
б) Всякая функция есть бинарное отношение.
Тема 3. ГРАФЫ
Первая работа по теории графов принадлежащая Эйлеру, появилась в 1736 году. Вначале эта теория была связана с математическими головоломками и играми. Однако впоследствии теория графов стала использоваться в топологии, алгебре, теории чисел. В наше время теория графов находит применение в самых разнообразных областях науки, техники и практической деятельности. Она используется при проектировании электрических сетей, планировании транспортных перевозок, построении молекулярных схем. Применяется теория графов также в экономике, психологии, социологии, биологии.