Топология – раздел математики, который занимается изучением пределов и непрерывностью функций. В соединении с алгеброй топология составляет общую основу математики.

Топологическое пространство или фигура – подмножество нашего однородного евклидового пространства, между точками которого задано некоторое отношение близости. Здесь рассматриваются фигуры не как жесткие тела, а как объекты, сделанные как бы из очень эластичной резины, допускающие непрерывную деформацию, сохраняющую их качественные свойства.

Взаимно-однозначное непрерывное отображение фигур называется гомеоморфизмом . Другими словами, фигуры гомеоморфны , если одну можно перевести в другую непрерывной деформацией.

Примеры. Гомеоморфны следующие фигуры (из разных групп фигуры не гомеоморфны), изображенные на рис. 2.

1. Отрезок и кривая без самопересечений.

2. Круг, внутренность квадрата, лента.

3. Сфера, поверхность куба и тетраэдра.

4. Окружность, эллипс и заузленная окружность.

5. Кольцо на плоскости (круг с дыркой), кольцо в пространстве, два раза перекрученное кольцо, боковая поверхность цилиндра.

6. Лист Мёбиуса, т.е. один раз перекрученное кольцо, и три раза перекрученное кольцо.

7. Поверхность тора (бублика), сфера с ручкой и заузленный тор.

8. Сфера с двумя ручками и крендель с двумя дырками.

В математическом анализе функции изучаются методом пределов. Переменная и предел – основные понятия.

В различных явлениях некоторые величины сохраняют свое численное значение, другие изменяются. Совокупность всех числовых значений переменной величины называется областью изменения этой переменной .

Из разнообразных способов поведения переменной величины наиболее важен такой, при котором переменная величина стремится к некоторому пределу.

Постоянное число a называется пределом переменной величиныx , если абсолютная величина разности между x иa () становится в процессе изменения переменной величины x сколь угодно малой:

Что значит « сколь угодно малой »? Переменная величина х стремится к пределу а ,если для любого сколь угодно малого (произвольно малого) числа найдется такой момент в изменении переменной х ,начиная с которого выполняется неравенство .

Определение предела имеет простой геометрический смысл: неравенство означает, что х находится в -окрестности точки a , т.е. в интервале .

Таким образом, определение предела можно дать в геометрической форме:

Число а является пределом переменной величины х , если для любой сколь угодно малой (произвольно малой) -окрестности числа а можно указать такой момент в изменении переменной х , начиная с которого все ее значения попадают в указанную -окрестность точки а .

Замечание . Переменная величина х может по-разному приближаться к своему пределу: оставаясь меньше этого предела (слева), больше (справа), колеблясь около значения предела.

Предел последовательности

Функцией называется закон (правило) по которому каждому элементу x некоторого множества X соответствует единственный элемент y множества Y.

Функция может быть задана на множестве всех натуральных чисел: . Такая функция называется функцией натурального аргумента или числовой последовательностью .

Так как последовательность, как и всякое бесконечное множество, нельзя задать перечислением, то она задается общим членом: , где – общий член последовательности.

Дискретной переменной называется общий член последовательности .

Для последовательности слова «начиная с некоторого момента» означают слова «начиная с некоторого номера».

Число а называется пределом последовательности , если для любого сколь угодно малого (произвольно малого) числа найдется такой номер N , что для всех членов последовательности с номером n >N выполняется неравенство .

или при .

Геометрически определение предела последовательности означает следующее: для любой сколь угодно малой (произвольно малой) -окрестности числа а найдется такой номер, что все члены последовательности с большими, чем N , номерами, попадают в эту окрестность. Вне окрестности оказывается лишь конечное число начальных членов последовательности. Натуральное число N зависит от : .

Понятие предела числовой последовательности

Вспомним сначала определение числовой последовательности.

Определение 1

Отображения множества натуральных чисел на множество действительных чисел называется числовой последовательностью .

Понятие предела числовой последовательности имеет несколько основных определений:

Действительное число $a$ называется пределом числовой последовательности $(x_n)$, если для любого $\varepsilon >0$ существует номер $N$, зависящий от $\varepsilon$, такой, что для любого номера $n> N$ выполняется неравенство $\left|x_n-a\right|
Действительное число $a$ называется пределом числовой последовательности $(x_n)$, если в любую окрестность точки $a$ попадают все члены последовательности $(x_n)$, за исключением, быть может, конечного числа членов.

Рассмотрим пример вычисления значения предела числовой последовательности:

Пример 1

Найти предел ${\mathop{lim}_{n\to \infty } \frac{n^2-3n+2}{2n^2-n-1}\ }$

Решение:

Для решения данного задания вначале нам необходимо вынести за скобки старшую степень, входящую в выражение:

${\mathop{lim}_{n\to \infty } \frac{n^2-3n+2}{2n^2-n-1}\ }={\mathop{lim}_{x\to \infty } \frac{n^2\left(1-\frac{3}{n}+\frac{2}{n^2}\right)}{n^2\left(2-\frac{1}{n}-\frac{1}{n^2}\right)}\ }={\mathop{lim}_{n\to \infty } \frac{1-\frac{3}{n}+\frac{2}{n^2}}{2-\frac{1}{n}-\frac{1}{n^2}}\ }$

Если в знаменателе стоит бесконечно большая величина, то весь предел стремится к нулю, $\mathop{lim}_{n\to \infty }\frac{1}{n}=0$, использовав это, получим:

${\mathop{lim}_{n\to \infty } \frac{1-\frac{3}{n}+\frac{2}{n^2}}{2-\frac{1}{n}-\frac{1}{n^2}}\ }=\frac{1-0+0}{2-0-0}=\frac{1}{2}$

Ответ: $\frac{1}{2}$.

Понятие предела функции в точке

Понятие предела функции в точке имеет два классических определения:

Определение термина «предел» по Коши

Действительное число $A$ называется пределом функции $f\left(x\right)$ при $x\to a$, если для любого $\varepsilon > 0$ существует $\delta >0$, зависящий от $\varepsilon $, такой, что для любого $x\in X^{\backslash a}$, удовлетворяющих неравенству $\left|x-a\right|

Определение по Гейне

Действительное число $A$ называется пределом функции $f\left(x\right)$ при $x\to a$, если для любой последовательности $(x_n)\in X$, сходящейся к числу $a$, последовательность значений $f(x_n)$ сходится к числу $A$.

Эти два определения связаны между собой.

Замечание 1

Определения предела функции по Коши и по Гейне эквивалентны.

Помимо классических подходов к вычислению пределов функции, вспомним формулы, которые могут также помочь в этом.

Таблица эквивалентных функций, когда $x$ бесконечно мал (стремится к нулю)

Одним из подходов к решению пределов является принцип замены на эквивалентную функцию . Таблица эквивалентных функций представлена ниже, чтобы ей воспользоваться, необходимо вместо функций справа подставить в выражение соответствующую элементарную функцию слева.

Рисунок 1. Таблица эквивалентности функций. Автор24 - интернет-биржа студенческих работ

Также для решения пределов, значения которых сводятся к неопределённости, возможно применить правило Лопиталя. В общем случае неопределённость вида $\frac{0}{0}$ можно раскрыть разложив на множители числитель и знаменатель и затем сократив. Неопределённость, имеющую форму $\frac{\infty }{\infty}$ возможно разрешить после деления выражений в числителе и знаментателе на переменную, при которой находится старшая степень.

Замечательные пределы

Первый замечательный предел:

${\mathop{lim}_{x\to 0} \frac{sinx}{x}\ }=1$

Второй замечательный предел:

$\mathop{lim}_{x\to 0}{(1+x)}^{\frac{1}{x}}=e$

Специальные пределы

Первый специальный предел:

$\mathop{lim}_{x\to 0}\frac{{{log}_a (1+x-)\ }}{x}={{log}_a e\ }=\frac{1}{lna}$

Второй специальный предел:

$\mathop{lim}_{x\to 0}\frac{a^x-1}{x}=lna$

Третий специальный предел:

$\mathop{lim}_{x\to 0}\frac{{(1+x)}^{\mu }-1}{x}=\mu $

Непрерывность функции

Определение 2

Функция $f(x)$ называется непрерывной в точке $x=x_0$, если $\forall \varepsilon >{\rm 0}$ $\exists \delta (\varepsilon ,E_{0})>{\rm 0}$ такое, что $\left|f(x)-f(x_{0})\right|

Функция $f(x)$ непрерывна в точке $х=х_0$, если $\mathop{{\rm lim\; }}\limits_{{\rm x}\to {\rm x}_{{\rm 0}} } f(x)=f(x_{0})$.

Точка $x_0\in X$ называется точкой разрыва первого рода, если в ней существуют конечные пределы ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }$, ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }$, но нарушается равенство ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }=f(x_0)$

Причем, если ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }={\mathop{lim}_{x\to x_0+0} f(x_0)\ }\ne f(x_0)$, то это точка устранимого разрыва, а если ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }\ne {\mathop{lim}_{x\to x_0+0} f(x_0)\ }$, то точка скачка функции.

Точка $x_0\in X$ называется точкой разрыва второго рода, если в ней хотя бы один из пределов ${\mathop{lim}_{x\to x_0-0} f(x_0)\ }$, ${\mathop{lim}_{x\to x_0+0} f(x_0)\ }$ представляет собой бесконечность или не существует.

Пример 2

Исследовать на непрерывность $y=\frac{2}{x}$

Решение:

${\mathop{lim}_{x\to 0-0} f(x)\ }={\mathop{lim}_{x\to 0-0} \frac{2}{x}\ }=-\infty $ - функция имеет точку разрыва второго рода.

Непрерывность функции. Точки разрыва.

Идет бычок, качается, вздыхает на ходу:
– Ох, доска кончается, сейчас я упаду!

На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность . Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно изучить статью и уловить все тонкости и технические приёмы.

Что нужно знать и уметь? Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции . Читателям с низким уровнем подготовки достаточно осмыслить статью Пределы функций. Примеры решений и посмотреть геометрический смысл предела в методичке Графики и свойства элементарных функций . Также желательно ознакомиться с геометрическими преобразованиями графиков , поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!

Непрерывность функции. Точки разрыва и их классификация

Понятие непрерывности функции

Рассмотрим некоторую функцию , непрерывную на всей числовой прямой:

Или, говоря лаконичнее, наша функция непрерывна на (множестве действительных чисел).

Каков «обывательский» критерий непрерывности? Очевидно, что график непрерывной функции можно начертить, не отрывая карандаша от бумаги.

При этом следует чётко отличать два простых понятия: область определения функции и непрерывность функции . В общем случае это не одно и то же . Например:

Данная функция определена на всей числовой прямой, то есть для каждого значения «икс» существует своё значение «игрека» . В частности, если , то . Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции: .

Однако эта функция не является непрерывной на ! Совершенно очевидно, что в точке она терпит разрыв . Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги. Немного позже мы рассмотрим классификацию точек разрыва.

Непрерывность функции в точке и на интервале

В той или иной математической задаче речь может идти о непрерывности функции в точке, непрерывности функции на интервале, полуинтервале или непрерывности функции на отрезке. То есть, не существует «просто непрерывности» – функция может быть непрерывной ГДЕ-ТО. И основополагающим «кирпичиком» всего остального является непрерывность функции в точке .

Теория математического анализа даёт определение непрерывности функции в точке с помощью «дельта» и «эпсилон» окрестностей, но на практике в ходу другое определение, которому мы и уделим самое пристальное внимание.

Сначала вспомним односторонние пределы , ворвавшиеся в нашу жизнь на первом уроке о графиках функций . Рассмотрим будничную ситуацию:

Если приближаться по оси к точке слева (красная стрелка), то соответствующие значения «игреков» будут идти по оси к точке (малиновая стрелка). Математически данный факт фиксируется с помощью левостороннего предела :

Обратите внимание на запись (читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует , по сути это и обозначает, что мы подходим к числу с левой стороны.

Аналогично, если приближаться к точке «ка» справа (синяя стрелка), то «игреки» придут к тому же значению , но уже по зелёной стрелке, и правосторонний предел оформится следующим образом:

«Добавка» символизирует , и запись читается так: «икс стремится к ка справа».

Если односторонние пределы конечны и равны (как в нашем случае): , то будем говорить, что существует ОБЩИЙ предел . Всё просто, общий предел – это наш «обычный» предел функции , равный конечному числу.

Заметьте, что если функция не определена при (выколите чёрную точку на ветке графика), то перечисленные выкладки остаются справедливыми. Как уже неоднократно отмечалось, в частности, в статье о бесконечно малых функциях , выражения означают, что «икс» бесконечно близко приближается к точке , при этом НЕ ИМЕЕТ ЗНАЧЕНИЯ , определена ли сама функция в данной точке или нет. Хороший пример встретится в следующем параграфе, когда анализу подвергнется функция .

Определение : функция непрерывна в точке , если предел функции в данной точке равен значению функции в этой точке: .

Определение детализируется в следующих условиях:

1) Функция должна быть определена в точке , то есть должно существовать значение .

2) Должен существовать общий предел функции . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: .

3) Предел функции в данной точке должен быть равен значению функции в этой точке: .

Если нарушено хотя бы одно из трёх условий, то функция теряет свойство непрерывности в точке .

Непрерывность функции на интервале формулируется остроумно и очень просто: функция непрерывна на интервале , если она непрерывна в каждой точке данного интервала.

В частности, многие функции непрерывны на бесконечном интервале , то есть на множестве действительных чисел . Это линейная функция, многочлены, экспонента, синус, косинус и др. И вообще, любая элементарная функция непрерывна на своей области определения , так, например, логарифмическая функция непрерывна на интервале . Надеюсь, к данному моменту вы достаточно хорошо представляете, как выглядят графики основных функций. Более подробную информацию об их непрерывности можно почерпнуть у доброго человека по фамилии Фихтенгольц.

С непрерывностью функции на отрезке и полуинтервалах тоже всё несложно, но об этом уместнее рассказать на уроке о нахождении минимального и максимального значений функции на отрезке , а пока голову забивать не будем.

Классификация точек разрыва

Увлекательная жизнь функций богата всякими особенными точками, и точки разрыва лишь одна из страничек их биографии.

Примечание : на всякий случай остановлюсь на элементарном моменте: точка разрыва – это всегда отдельно взятая точка – не бывает «несколько точек разрыва подряд», то есть, нет такого понятия, как «интервал разрывов».

Данные точки в свою очередь подразделяются на две большие группы: разрывы первого рода и разрывы второго рода . У каждого типа разрыва есть свои характерные особенности, которые мы рассмотрим прямо сейчас:

Точка разрыва первого рода

Если в точке нарушено условие непрерывности и односторонние пределы конечны , то она называется точкой разрыва первого рода .

Начнём с самого оптимистичного случая. По первоначальной задумке урока я хотел рассказать теорию «в общем виде», но чтобы продемонстрировать реальность материала, остановился на варианте с конкретными действующими лицами.

Уныло, как фото молодожёнов на фоне Вечного огня, но нижеследующий кадр общепринят. Изобразим на чертеже график функции :

Данная функция непрерывна на всей числовой прямой, кроме точки . И в самом деле, знаменатель же не может быть равен нулю. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают:
(Условие №2 непрерывности выполнено).

Но функция не определена в точке , следовательно, нарушено Условие №1 непрерывности, и функция терпит разрыв в данной точке.

Разрыв такого вида (с существующим общим пределом ) называют устранимым разрывом . Почему устранимым? Потому что функцию можно доопределить в точке разрыва:

Странно выглядит? Возможно. Но такая запись функции ничему не противоречит! Теперь разрыв устранён и все счастливы:

Выполним формальную проверку:

2) – общий предел существует;
3)

Таким образом, все три условия выполнены, и функция непрерывна в точке по определению непрерывности функции в точке.

Впрочем, ненавистники матана могут доопределить функцию нехорошим способом, например :

Любопытно, что здесь выполнены первые два условия непрерывности:
1) – функция определена в данной точке;
2) – общий предел существует.

Но третий рубеж не пройден: , то есть предел функции в точке не равен значению данной функции в данной точке.

Таким образом, в точке функция терпит разрыв.

Второй, более грустный случай носит название разрыва первого рода со скачком . А грусть навевают односторонние пределы, которые конечны и различны . Пример изображён на втором чертеже урока. Такой разрыв возникает, как правило, в кусочно-заданных функциях , о которых уже упоминалось в статье о преобразованиях графиков .

Рассмотрим кусочную функцию и выполним её чертёж. Как построить график? Очень просто. На полуинтервале чертим фрагмент параболы (зеленый цвет), на интервале – отрезок прямой (красный цвет) и на полуинтервале – прямую (синий цвет).

При этом в силу неравенства значение определено для квадратичной функции (зелёная точка), и в силу неравенства , значение определено для линейной функции (синяя точка):

В самом-самом тяжёлом случае следует прибегнуть к поточечному построению каждого куска графика (см. первый урок о графиках функций ).

Сейчас нас будет интересовать только точка . Исследуем её на непрерывность:

2) Вычислим односторонние пределы.

Слева у нас красный отрезок прямой, поэтому левосторонний предел:

Справа – синяя прямая, и правосторонний предел:

В результате получены конечные числа , причем они не равны . Поскольку односторонние пределы конечны и различны : , то наша функция терпит разрыв первого рода со скачком .

Логично, что разрыв не устраним – функцию действительно не доопределить и «не склеить», как в предыдущем примере.

Точки разрыва второго рода

Обычно к данной категории хитро относят все остальные случаи разрыва. Всё перечислять не буду, поскольку на практике в 99%-ти процентах задач вам встретится бесконечный разрыв – когда левосторонний или правосторонний, а чаще, оба предела бесконечны.

И, конечно же, самая напрашивающаяся картинка – гипербола в точке ноль. Здесь оба односторонних предела бесконечны: , следовательно, функция терпит разрыв второго рода в точке .

Я стараюсь наполнять свои статьи максимально разнообразным содержанием, поэтому давайте посмотрим на график функции , который ещё не встречался:

по стандартной схеме:

1) Функция не определена в данной точке, поскольку знаменатель обращается в ноль.

Конечно, можно сразу сделать вывод о том, что функция терпит разрыв в точке , но хорошо бы классифицировать характер разрыва, что часто требуется по условию. Для этого:

Напоминаю, что под записью понимается бесконечно малое отрицательное число , а под записью – бесконечно малое положительное число .

Односторонние пределы бесконечны, значит, функция терпит разрыв 2-го рода в точке . Ось ординат является вертикальной асимптотой для графика.

Не редка ситуация, когда оба односторонних предела существуют, но бесконечен только один из них, например:

Это график функции .

Исследуем на непрерывность точку :

1) Функция не определена в данной точке.

2) Вычислим односторонние пределы:

О методике вычисления таких односторонних пределов поговорим в двух последних примерах лекции, хотя многие читатели всё уже увидели и догадались.

Левосторонний предел конечен и равен нулю (в саму точку мы «не заходим»), но правосторонний предел бесконечен и оранжевая ветка графика бесконечно близко приближается к своей вертикальной асимптоте , заданной уравнением (чёрный пунктир).

Таким образом, функция терпит разрыв второго рода в точке .

Как и для разрыва 1-го рода, в самой точке разрыва функция может быть определена. Например, для кусочной функции смело ставим чёрную жирную точку в начале координат. Справа же – ветка гиперболы, и правосторонний предел бесконечен. Думаю, почти все представили, как выглядит этот график.

То, чего все с нетерпением ждали:

Как исследовать функцию на непрерывность?

Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:

Пример 1

Исследовать функцию

Решение :

1) Под прицел попадает единственная точка , в которой функция не определена.

2) Вычислим односторонние пределы:

Односторонние пределы конечны и равны.

Таким образом, в точке функция терпит устранимый разрыв.

Как выглядит график данной функции?

Хочется провести упрощение , и вроде бы получается обычная парабола. НО исходная функция не определена в точке , поэтому обязательна следующая оговорка:

Выполним чертёж:

Ответ : функция непрерывна на всей числовой прямой кроме точки , в которой она терпит устранимый разрыв.

Функцию можно доопределить хорошим или не очень способом, но по условию этого не требуется.

Вы скажете, пример надуманный? Ничуть. Десятки раз встречалось на практике. Почти все задачи сайта родом из реальных самостоятельных и контрольных работ.

Разделаемся с любимыми модулями:

Пример 2

Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.

Решение : почему-то студенты боятся и не любят функции с модулем, хотя ничего сложного в них нет. Таких вещей мы уже немного коснулись на уроке Геометрические преобразования графиков . Поскольку модуль неотрицателен, то он раскрывается следующим образом: , где «альфа» – некоторое выражение. В данном случае , и наша функция должна расписаться кусочным образом:

Но дроби обоих кусков предстоит сократить на . Сокращение, как и в предыдущем примере, не пройдёт без последствий. Исходная функция не определена в точке , так как знаменатель обращается в ноль. Поэтому в системе следует дополнительно указать условие , и первое неравенство сделать строгим:

Теперь об ОЧЕНЬ ПОЛЕЗНОМ приёме решения : перед чистовым оформлением задачи на черновике выгодно сделать чертёж (независимо от того, требуется он по условию или нет). Это поможет, во-первых, сразу увидеть точки непрерывности и точки разрыва, а, во-вторых, 100%-но убережёт от ошибок при нахождении односторонних пределов.

Выполним чертёж. В соответствии с нашими выкладками, слева от точки необходимо начертить фрагмент параболы (синий цвет), а справа – кусок параболы (красный цвет), при этом функция не определена в самой точке :

Если есть сомнения, возьмите несколько значений «икс», подставьте их в функцию (не забывая, что модуль уничтожает возможный знак «минус») и сверьтесь с графиком.

Исследуем функцию на непрерывность аналитически:

1) Функция не определена в точке , поэтому сразу можно сказать, что не является в ней непрерывной.

2) Установим характер разрыва, для этого вычислим односторонние пределы:

Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке . Ещё раз заметьте, что при нахождении пределов не имеет значения, определена функция в точке разрыва или нет.

Теперь остаётся перенести чертёж с черновика (он сделан как бы с помощью исследования;-)) и завершить задание:

Ответ : функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв первого рода со скачком.

Иногда требуют дополнительно указать скачок разрыва. Вычисляется он элементарно – из правого предела нужно вычесть левый предел: , то есть в точке разрыва наша функция прыгнула на 2 единицы вниз (о чём нам сообщает знак «минус»).

Пример 3

Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.

Это пример для самостоятельного решения, примерный образец решения в конце урока.

Перейдём к наиболее популярной и распространённой версии задания, когда функция состоит из трёх кусков:

Пример 4

Исследовать функцию на непрерывность и построить график функции .

Решение : очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике, технику построения я достаточно подробно закомментировал в первой части статьи. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства значение принадлежит прямой (зелёная точка), и в силу неравенство значение принадлежит параболе (красная точка):

Ну вот, в принципе, всё понятно =) Осталось оформить решение. Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:

I) Исследуем на непрерывность точку

Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .

Вычислим скачок разрыва как разность правого и левого пределов:
, то есть, график рванул на одну единицу вверх.

II) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Найдём односторонние пределы:

– односторонние пределы конечны и равны, значит, существует общий предел.

3) – предел функции в точке равен значению данной функции в данной точке.

На завершающем этапе переносим чертёж на чистовик, после чего ставим финальный аккорд:

Ответ : функция непрерывна на всей числовой прямой, кроме точки , в которой она терпит разрыв первого рода со скачком.

Пример 5

Исследовать функцию на непрерывность и построить её график .

Это пример для самостоятельного решения, краткое решение и примерный образец оформления задачи в конце урока.

Может сложиться впечатление, что в одной точке функция обязательно должна быть непрерывной, а в другой – обязательно должен быть разрыв. На практике это далеко не всегда так. Постарайтесь не пренебрегать оставшимися примерами – будет несколько интересных и важных фишек:

Пример 6

Дана функция . Исследовать функцию на непрерывность в точках . Построить график.

Решение : и снова сразу выполним чертёж на черновике:

Особенность данного графика состоит в том, что при кусочная функция задаётся уравнением оси абсцисс . Здесь данный участок прорисован зелёным цветом, а в тетради его обычно жирно выделяют простым карандашом. И, конечно же, не забываем про наших баранов: значение относится к ветке тангенса (красная точка), а значение принадлежит прямой .

Из чертежа всё понятно – функция непрерывна на всей числовой прямой, осталось оформить решение, которое доводится до полного автоматизма буквально после 3-4 подобных примеров:

I) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Вычислим односторонние пределы:

, значит, общий предел существует.

На всякий пожарный напомню тривиальный факт: предел константы равен самой константе. В данном случае предел нуля равен самому нулю (левосторонний предел).

3) – предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.

II) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Найдём односторонние пределы:

И здесь – предел единицы равен самой единице.

– общий предел существует.

3) 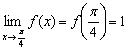– предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.

Как обычно, после исследования переносим наш чертёж на чистовик.

Ответ : функция непрерывна в точках .

Обратите внимание, что в условии нас ничего не спрашивали про исследование всей функции на непрерывность, и хорошим математическим тоном считается формулировать точный и чёткий ответ на поставленный вопрос. Кстати, если по условию не требуется строить график, то вы имеете полное право его и не строить (правда, потом преподаватель может заставить это сделать).

Небольшая математическая «скороговорка» для самостоятельного решения:

Пример 7

Дана функция . Исследовать функцию на непрерывность в точках . Классифицировать точки разрыва, если они есть. Выполнить чертёж.

Постарайтесь правильно «выговорить» все «слова» =) И график нарисовать поточнее, точность, она везде лишней не будет;-)

Как вы помните, я рекомендовал незамедлительно выполнять чертёж на черновике, но время от времени попадаются такие примеры, где не сразу сообразишь, как выглядит график. Поэтому в ряде случаев выгодно сначала найти односторонние пределы и только потом на основе исследования изобразить ветви. В двух заключительных примерах мы, кроме того, освоим технику вычисления некоторых односторонних пределов:

Пример 8

Исследовать на непрерывность функцию и построить её схематический график.

Решение : нехорошие точки очевидны: (обращает в ноль знаменатель показателя) и (обращает в ноль знаменатель всей дроби). Малопонятно, как выглядит график данной функции, а значит, сначала лучше провести исследование.

Предел и непрерывность

функции одной переменной

3.1.1. Определение. Число А x стремящимся к x 0 , если для любого числа
найдётся число
(
), и будет выполняться условие:

если
, то
.

(Символика:
).

Если точки графика Г функции

, когда неограниченно близко приближается к точке (т.е.
), (см. Рис. 3.1), то это обстоятельство является геометрическим эквивалентом того, что функция
при
имеет предельное значение (предел) A (символика:
).

График функции ,

Рис. 3.1

Следует отметить, что в определении предельного значения (предела) функции при x стремящемся к x 0 ничего не говорится о поведении функции в точке x 0 . В самой точке x 0 функция может быть не определена, может быть
, а может быть
.

Если
, то функция называется бесконечно малой при
.

Промежуток называют  - окрестностью точки x 0 с выколотым центром. Используя это название, можно сказать так: , если для любого числа найдётся число , и будет выполняться условие: если
, то
.

3.1.2. Определение. , если для любой сходящейся к x 0 последовательности
последовательность
сходится к А .

3.1.3. Докажем эквивалентность определений разделов 3.1.1 и 3.1.2

Пусть сначала в смысле первого определения и пусть
(
), тогда все , кроме их конечного числа удовлетворяют неравенству
, где  выбрано по  в смысле первого определения, т.е.
, т.е. из первого определения следует второе. Пусть теперь
в смысле второго определения и допустим, что в смысле второго определения
, т.е. для некоторого при сколь угодно малых (например, при
) нашлась последовательность
, но при этом
. Пришли к противоречию, следовательно, из второго определения следует первое.

3.1.4. Эквивалентность этих определений особенно удобна, ибо все доказанные ранее теоремы о свойствах пределов для последовательностей переносятся почти автоматически на новый случай. Следует лишь уточнить понятие ограниченности. Соответствующая теорема имеет следующую формулировку:

Если
, то ограничена на некоторой  - окрестности точки x 0 с выколотым центром.

3.2.1.Теорема. Пусть
,
,

тогда,
,

3.2.2. Пусть

- произвольная, сходящаяся к x 0 последовательность значений аргументов функций и
. Соответствующие последовательности
и
значений этих функций имеют пределы A и B . Но тогда, в силу теоремы раздела 2.13.2, последовательности
,
и
имеют пределы, соответственно равные A +B ,
и
. Согласно определению предела функции в точке (см. раздел 2.5.2) это означает, что

,
,

3.2.3. Теорема. Если
,
, и в некоторой окрестности

имеет место

3.2.4. По определению предела функции в точке x 0 для любой последовательности
такой, что

последовательность значений функции имеет предел равный А . Это означает, что для любого
существует номер
выполняется . Аналогично, для последовательности
существует номер
такой, что для любого номера
выполняется . Выбирая
, получаем, что для всех
выполняется . Из этой цепочки неравенств имеем для любого , что означает, что
.

3.2.5. Определение. Число А называется предельным значением (пределом) функции при x стремящимся к x 0 справа (символика:
), если для любого числа найдётся число () и будет выполняться условие: если
, то
.

Множество называют правой  - окрестностью точки x 0 . Аналогично определяется понятие предельного значения (предела) слева (
).

3.2.6. Теорема. Функция при имеет предельное значение (предел) равный А тогда и только тогда, когда

3.3.1. Определение. Число А называется предельным значением (пределом) функции при x стремящимся к бесконечности, если для любого числа найдётся число
(
) и будет выполняться условие:

если
, то .

(Символика:
.)

Множество
называется D -окрестностью бесконечности.

3.3.2. Определение. Число А называется предельным значением (пределом) функции при x стремящимся к плюс бесконечности, если для любого числа найдётся число D () и будет выполняться условие:

если
, то .

(Символика:
).

Если точки графика Г функции
с неограниченным ростом
неограниченно приближаются к единственной горизонтальной прямой
(см. Рис. 3.2), то это обстоятельство является геометрическим эквивалентом того, что функция
при
имеет предельное значение (предел), равное числу A (символика:
).

График функции
,

Множество
называется D -окрестностью плюс бесконечности.

Аналогично определяется понятие предела при
.

Упражнения.

Сформулируйте все теоремы о пределах применительно к случаям:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. Определение. Функция называется бесконечно большой функцией (или просто бесконечно большой) при , если для любого числа

, удовлетворяющих неравенству , выполняется неравенство
.

(Символика:
.)

Если выполняется
, то пишут
.

3.4.2. Теорема. Пусть
и
при
.

Тогда
- бесконечно большая функция при .

3.4.3. Пусть произвольное число . Так как - бесконечно малая функция при , то для числа
существует число такое, что для всех x таких, что выполняется неравенство
, но тогда для тех же x выполнятся неравенство
. Т.е. - бесконечно большая функция при .

3.4.4.Теорема. Пусть - бесконечно большая функция при и при .

Тогда - бесконечно малая функция при .

(Эта теорема доказывается аналогично теореме раздела 3.8.2).

3.4.5. Функция
называется неограниченной при
, если для любого числа
и любой δ-окрестности точки можно указать точку x из этой окрестности такую, что
.

3.5.1. ОПРЕДЕЛЕНИЕ. Функция называется непрерывной в точке , если
.

Последнее условие можно записать и так:

Эта запись означает, что для непрерывных функций можно менять местами знак предела и знак функции

Или так: . Или снова, как в начале.

Обозначим
. Тогда
и =
и последняя форма записи примет вид

Выражение под знаком предела представляет собой приращение функции точке , вызванное приращением
аргумента x в точке , обозначаемое обычно как
. В итоге получаем следующую форму записи условия непрерывности функции в точке

которую называют «рабочим определением» непрерывности функции в точке.

Функция называется непрерывной в точке слева , если
.

Функция называется непрерывной в точке справа , если
.

3.5.2. Пример.
. Эта функция непрерывна для любого . С помощью теорем о свойствах пределов, мы сразу получаем: любая рациональная функция непрерывна в каждой точке, в которой она определена, т.е. функция вида
.

УПРАЖНЕНИЯ .

3.6.1. В школьном учебнике доказывается (на высоком уровне строгости), что
(первый замечательный предел). Из наглядных геометрических соображений сразу получается, что
. Заметим, что из левого неравенства следует также, что
, т.е. что функция
непрерывна в нуле. Отсюда уж совсем нетрудно доказать непрерывность всех тригонометрических функций во всех точках, где они определены. В самом деле, при
как произведение бесконечно малой функции
на ограниченную функцию
.

3.6.2. (2-й замечательный предел). Как нам уже известно

где пробегает натуральные числа. Можно показать, что
. Более того
.

УПРАЖНЕНИЯ .

3.7.1. ТЕОРЕМА (о непрерывности сложной функции).

Если функция
непрерывна в точке и
, а функция
непрерывна в точке , то сложная функция
непрерывна в точке .

3.7.2. Справедливость этого утверждения немедленно следует из определения непрерывности, записанного в виде:

3.8.1. ТЕОРЕМА. Функция непрерывна в каждой точке (
).

3.8.2. Если считать обоснованным, что функция
определена для любого и является строго монотонной (строго убывающей при
, строго возрастающей при
), то доказательство не составляет труда.

При
имеем:

т.е. при имеем
, что означает, что функция непрерывна при .

При
всё сводится к предыдущему:

При
.

При
функция
постоянна при всех , следовательно, непрерывна.

3.9.1. ТЕОРЕМА (о сосуществовании и непрерывности обратной функции).

Пусть непрерывная функция строго убывает (строго возрастает) в некоторой δ - окрестности точки ,
. Тогда в некоторой ε - окрестности точки существует обратная функция
, которая строго убывает (строго возрастает) и непрерывна в ε - окрестности точки .

3.9.2. Докажем здесь только непрерывность обратной функции в точке .

Возьмём , точка y расположена между точками
и
, следовательно, если
, то
, где .

3.10.1. Итак, любые позволительные арифметические действия над непрерывными функциями вновь приводят к непрерывным функциям. Образование из них сложных и обратных функций не портит непрерывности. Поэтому, с некоторой долей ответственности, мы можем утверждать, что все элементарные функции при всех допустимых значениях аргумента непрерывны.

УПРАЖНЕНИЕ .

Докажите, что
при
(другая форма второго замечательного предела).

3.11.1. Вычисление пределов сильно упрощается, если использовать понятие эквивалентных бесконечно малых. Понятие эквивалентности удобно обобщить на случай произвольных функций.

Определение. Функции и называются эквивалентными при , если
(вместо можно писать
,
,
,
,
).

Используемое обозначение f ~ g .

Эквивалентность обладает следующими свойствами

Необходимо помнить следующий список эквивалентных бесконечно малых:

~
при
; (1)

~ при ; (2)

~
при ; (3)

~ при ; (4)

~ при ; (5)

~ при ; (6)

~ при ; (7)

~ p при ; (8)

~ при
; (9)

~
при . (10)

Здесь и могут быть не независимыми переменными, а функциями
и
стремящимися соответственно к нулю и единице при некотором поведении x . Так, например,

~
при
,

~
при
.

Эквивалентность (1) является иной формой записи первого замечательного предела. Эквивалентности (2), (3), (6) и (7) можно доказать непосредственно. Эквивалентность (4) получается из (1) с учётом свойства 2) эквивалентностей:

~
.

Аналогично (5) и (7) получаются из (2) и (6). В самом деле

~
,

~
.

Эквивалентность (8) доказывается последовательным применением (7) и (6):

а (9) и (10) получаются из (6) и (8) заменой
.

3.11.2. Теорема. При вычислении пределов в произведении и отношении можно менять функции на эквивалентные. А именно, если ~
, то, либо оба предела не существуют одновременно, и
, либо оба эти предела не существуют одновременно.

Докажем первое равенство. Пусть один из пределов, скажем,
существует. Тогда

3.11.3. Пусть (- число или символ ,
или
). Будем рассматривать поведение различных б.м. функций (так будем сокращать термин бесконечно малая).

ОПРЕДЕЛЕНИЯ.
и называются эквивалентными б.м. функциями при , если
(при ).

будем называть б.м. более высокого порядка чем б.м. функция
, если
(при ).

3.11.4. Если и эквивалентные б.м. функции, то
есть б.м. функция более высокого порядка чем
и чем . - б.м. функции при, в которой для всех x и, если в этой точке функция называется точкой устранимого разрыва. имеет разрыв второго рода. Сама точкаКонтрольная работа

К коллоквиуму. Разделы: «Предел и непрерывность функции действительной переменной» функции одной переменной» , «Дифференциальное исчисление функций нескольких переменных»

Тематика и примеры контрольных заданий и вопросов (контрольные работы индивидуальные типовые расчеты коллоквиум) i семестр контрольная работа №1 раздел «предел и непрерывность функции действительной переменной»

Контрольная работа

К коллоквиуму. Разделы: «Предел и непрерывность функции действительной переменной» , «Дифференциальное исчисление функции одной переменной» , «Дифференциальное исчисление функций нескольких переменных» . Числовая последовательность...

Контрольная работа

Тематика и примеры контрольных заданий и вопросов (контрольная работа индивидуальные типовые расчеты коллоквиумы) i семестр контрольная работа раздел «предел и непрерывность функции действительной переменной»

Контрольная работа

Лекция 19 предел и непрерывность функции нескольких переменных

Лекция

... Предел и непрерывность функции нескольких переменных . 19.1. Понятие функции нескольких переменных . При рассмотрении функций нескольких переменных ... свойствам функций одной переменной , непрерывных на отрезке. См. Свойства функций , непрерывных на...